数理统计笔记：假设检验（I）序言

笑看风云

本小节旨在阐述：

• 假设检验的定义及数学原理；
  
• 两类错误的定义及降低错误的一般准则；
  
• 介绍两类检验的求法，似然比检验和并-交检验 / 交-并检验。
  

1. 什么是假设检验？

假设 (hypothesis testing) 是关于总体参数的一个陈述。一个假设检验问题中两个互补的假设称为原假设 H_0 (null hypothesis)和备择假设 H_1 (alternative hypothesis)。若 \theta 表示一个总体参数，原假设和备择假设的一般格式为 H_0: \theta \in \Theta_0 \sim H_1: \theta \in \Theta_1 ,其中 \Theta_0 表示参数空间的某子集， \Theta_1 是 \Theta_0 的补集。一个假设检验问题中，试验者观测到样本之后必须决定拒绝 H_0 与否。
进行决策需要给出如何利用样本信息的规则，即“对于哪些样本值应该拒绝 H_0 ，哪些样本不能拒绝 H_0 ”。很自然地，可以利用样本的函数，检验统计量 T(X_1, X_2, \cdots, X_n) = T(X) 来确定。如“当 T(X) > 1 时，拒绝 H_0 ”就是一个检验， W= \{(x_1, x_2, \cdots, x_n): T(x) >1\} 就称为该检验的拒绝域。
\blacktriangleright Note:

• 二选一问题。假设检验问题是一个二选一的问题，将总体参数空间分割成两个不相交的部分，根据样本进行决策参数应该属于哪个空间。
  
• 不对等关系。利用样本决策能否拒绝 H_0 ，暗含着 H_0 和 H_1 的关系不是对等的： H_0 生来就是要被拒绝的。这一点类似法庭上的原告和被告，被告无罪相当于 H_0 ，在“无罪推定”的前提下需要找到证据推翻 H_0 ，即证明被告有罪。需要注意“不能拒绝 H_0 ”和“接受 H_0 ”似乎是同一种决策，但是有细微的差别，就好像“没有证据证明罪犯有罪”和“真的无罪”之间的不同。
  
• 区分参数空间和样本空间。在假设检验问题中，既将参数空间分割成两个部分， \Theta=\Theta_0 \cup \Theta_1 ，将样本空间分割成两个部分， S = S_0 \cup S_1，其中 S_1 为拒绝域。注意这两种分割有关但不同，若样本 X 落在拒绝域 S_1 ，则拒绝 \Theta \in \Theta_0 。  \blacktriangleleft
  

2. 假设检验的数学本质

从数学上讲，解决假设检验问题需要用到“反证法”：构造一个小概率事件，进行一次试验，如果小概率事件发生了，则违背了“一次试验中小概率事件不发生的原理”，拒绝原假设。典型的例子是由罗纳德·艾尔默·费歇尔 (R. A. Fisher) 提出的“女士品茶”的例子。
一位女士 (Muriel Bristol) 坚称自己能够分辨一杯茶是先放奶 (M)还是先放茶 (T)。为了检验这位女士是否真的有品鉴能力，Fisher首先引入了一个假设， H_0：女士没有品鉴能力。由此，在此假设下，构造一个小概率事件。

• 先取8个完全相同的杯子，每杯含体积相同的奶和茶，其中4个杯子先倒茶后倒牛奶 (TM)，4个杯子先倒牛奶后倒茶 (MT)，把8个杯子随机排成一列；
  
• 让这位女士品鉴这8杯茶，并选出 TM 的四杯。如果该女士没有品鉴能力（她完全瞎猜），那么她8杯全部猜中的概率是  1/70 \approx 0.0143，可认为此事件为小概率事件。
  
• 如果这位女士猜对了全部4杯，小概率事件发生，推翻原假设，可以认为此女士有品鉴能力。
  

假定原假设成立，构造小概率事件，进行试验，判断是否拒绝原假设，完成整个假设检验的推演。
\blacktriangleright Note:

• 何为小概率？到底多小才算小概率呢？Fisher当时给出了一个值，小于 1/20 =0.05 时可认为小概率事件。这个0.05一直沿用下来，需注意0.05不是黄金标准，具体情况还需具体分析。
  
• 概率分布。设 X 中表示是女士选对 TM 的杯数，则 X 服从超几何分布，故 P(X = 4) = \binom{4}{4}\binom{4}{0} / \binom{8}{4} = 1/70 . 若女士猜对了3杯，那么 P(X = 3) = \binom{4}{3}\binom{4}{1} / \binom{8}{4} = 16/70 \approx 0.229 > 0.05, 不能拒绝原假设，即便女士瞎猜，蒙对3杯也不是稀奇的事情。 \blacktriangleleft
  

3. 两类错误

将上述原理应用到一般的假设检验问题中，需要引入两类错误的概念。对于二分类问题，总是会有以下两种错误：



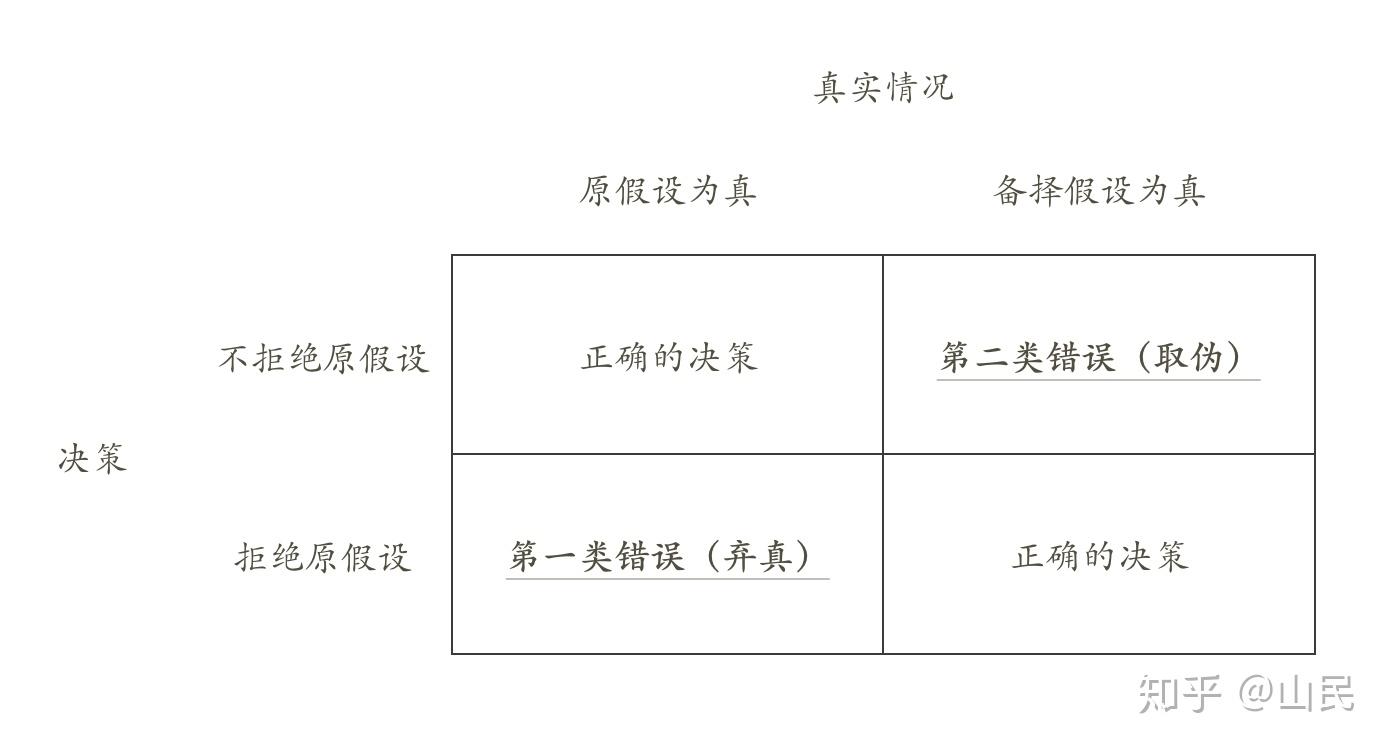
第一类错误和第二类错误

我们当然希望第一类错误 \alpha 和第二类错误 \beta 都尽量地小，但这是不可能的。下面举一个例子：
例：假设 X \sim \mathcal{N}(\mu, 1) 服从正态分布，其中 \mu 未知，抽出16个样本。
进行如下检验，H_0: \mu = 2 \sim H_1: \mu \ge 2 . 假定得到拒绝域为 W= \{\overline{X} \ge 2.41\} ，则
\alpha = P(\overline{X} \ge 2.41| \mu = 2) = P(4(\overline{X}-2) >1.64)=0.05.
第二类错误需要在 H_1 成立下进行，不妨假设 \mu=2.2 ，则
\beta = P(\overline{X} < 2.41| \mu = 2.2) = P(4(\overline{X}-2.2) <0.84 )\approx 0.80.



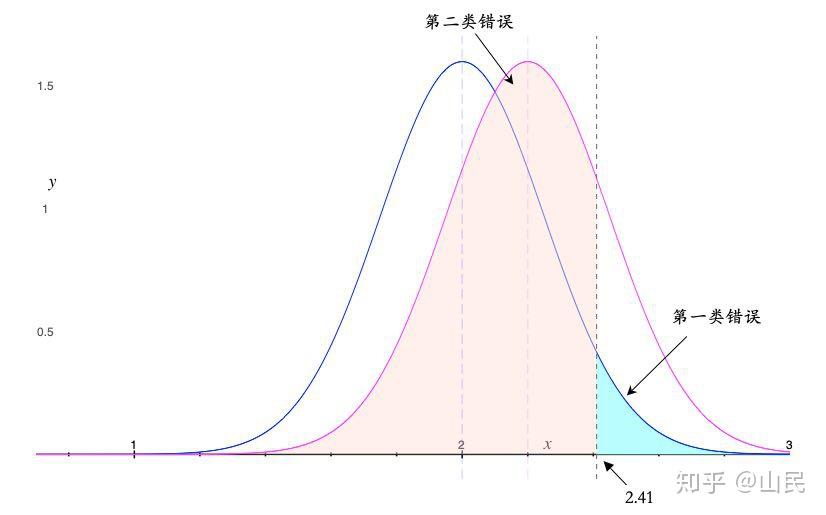
第一类错误与第二类错误之间的关系

上图很好地说明二者的关系，如果减小第一类错误 \alpha ，即将 x=2.41 这条线向右移，左边粉色区域就会增加，即第二类错误 \beta 增加。既然无法同时降低两类错误，现在比较公认的做法是：先控制第一类错误 \alpha 到一个较小的概率，再进一步降低第二类错误 \beta 。
由此，对 \alpha 的控制就潜在地构造了一个小概率事件，即 P(T \in W | H_0) \le \alpha . 据此，可以反推拒绝域 W ，再根据样本信息进行决策。
\blacktriangleright Note:

• 在控制住 \alpha 之后，如何降低 \beta 呢？可以引入功效（势，power）的概念，对于一个检验，将 1-\beta 定义为检验的功效。一个好的检验就是在 \alpha 固定下，尽量选择功效大的检验。依旧举上面的例子，其功效为：
  

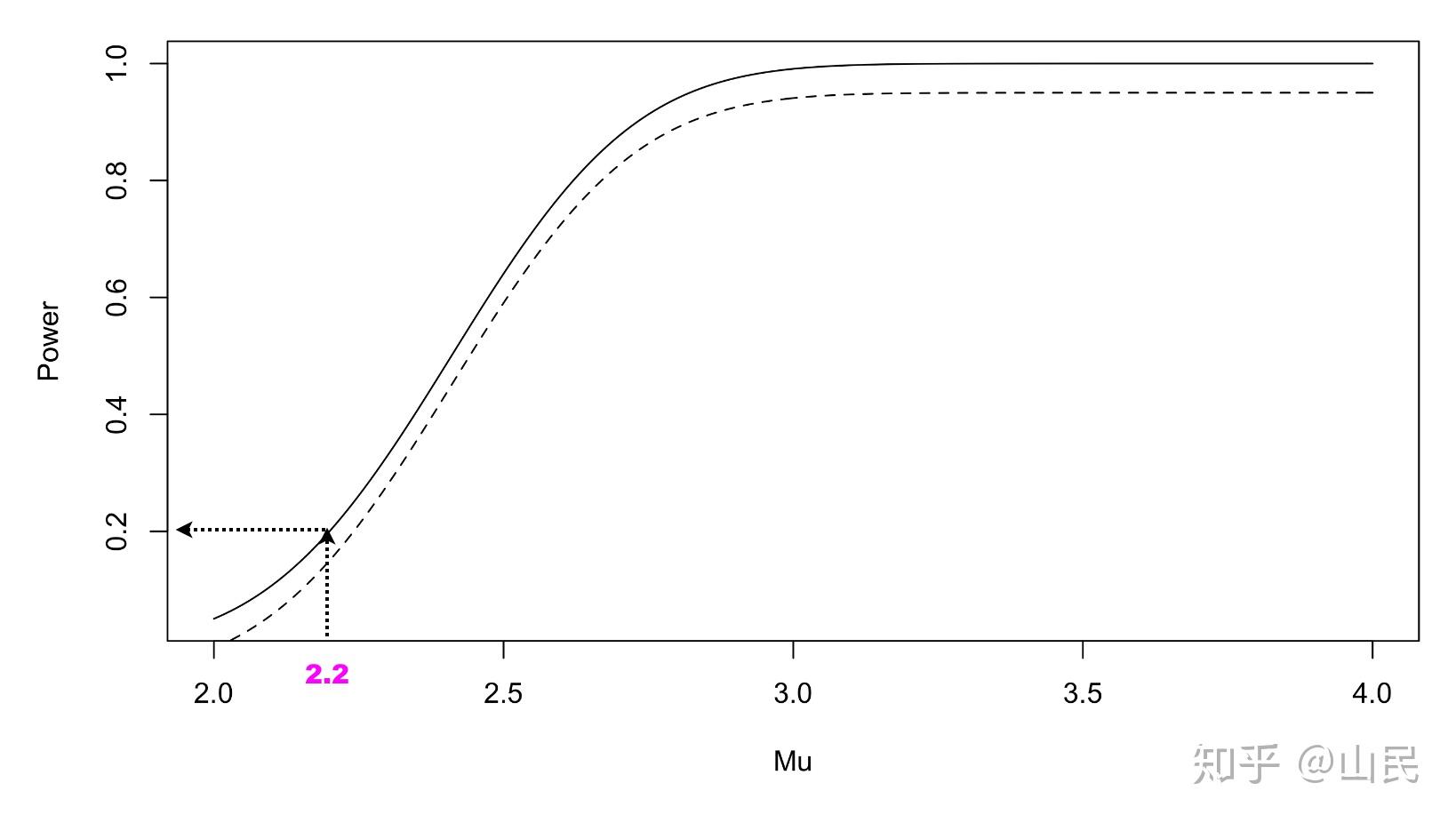
检验的功效，实线为例子中检验的功效，虚线为另一个检验的功效

• 实线和虚线分别代表两个检验，根据规则，显然应该选择实线对应的检验，由此一个好的检验，其功效往往是一致地 (uniformly) 大于其他检验，我们称其为一致最大功效检验 (uniformly most powerful tests)。 \blacktriangleleft
  

4. 一种检验的求法：似然比检验

假设检验： H_0: \theta \in \Theta_0 \sim H_1: \theta \in \Theta_1 ，设 n 个样本的似然函数为 f_n(x) ，则构造似然比 (likelihood ratio) 统计量：
\begin{equation*} \Lambda (x) = \frac{sup_{\theta \in \Theta_0} f_n(x|\theta)}{sup_{\theta \in \Theta} f_n(x|\theta)} \end{equation*}，
似然比检验的拒绝区域为 W= \{\Lambda(x) \le k\} 。给定第一类错误 \alpha=0.05 ，令 P(\Lambda(y) \le k | H_0) \le 0.05  求得相应的 k ，得到检验的拒绝域。
\dagger 例[1]：设 Y \sim B(n,\theta) , 其中 n=10 , \theta 未知。考察检验 H_0: \theta  = 0.3 \sim H_1: \theta \neq 0.3，确定拒绝域。
解：似然函数为 f(y|\theta) = \binom{n}{y} \theta^y (1-\theta)^{n-y}. 似然比统计量为 \begin{equation*} \Lambda (x) = \frac{0.3^y \times0.7^{n-y}}{sup_{\theta \in [0,1] \theta^y (1-\theta)^{n-y}}} \end{equation*} . 对于分母，可利用极大似然估计代替 \hat{\theta} = y/n. 所以, \begin{equation} \Lambda(y)=\big( \frac{0.3n}{y} \big)^y \big( \frac{0.7n}{n-y} \big)^{n-y}.  \end{equation} 这时令 \begin{equation} P(\Lambda(y) \le k) \le 0.05 \end{equation} , 计算出如下分布：



似然比及其概率分布

由此，当 y \in \{10, 9, 8, 7 \} 时，概率约为 0.039 ，一旦加入 y=6 ，概率增加到 0.076>0.05，不符合 P(\Lambda(y) \le k | H_0) \le 0.05 的规定，故拒绝域为 W = \{y: y\in \{10, 9, 8, 7 \}\} 。 \dagger
\blacktriangleright Note:

• 拒绝域为何是小于等于的形式？设想如果似然函数的极大值在 \Theta_0 空间取到，显然似然比是 1 ；如果在 \Theta_1 空间取到则似然比越远离 1 ，就应该越拒绝原假设。显然，拒绝域就该取小于等于的形式。
  
• 一个小技巧。似然比统计量的分布往往难以计算，可以将其转换为已知分布或密度的随机变量，再求其拒绝域。 \blacktriangleleft
  

5. 另一种检验的求法：并-交检验 / 交-并检验

除了似然比检验外，还有其他检验的求法，对于某种复杂原假设能够从简单原假设 (单点集) 推出。如当原假设可以表示为一个交集时，可以用并-交检验 (union-intersection method)来解决。 设 H_0: \theta \in \cap_{\gamma \in \Gamma} \Theta_{\gamma}   ，其中 \Gamma 是任意的指标集合，可能有限也可能无限。如果对于每个检验问题 H_{0\gamma}: \theta \in \Theta_{\gamma}  \sim H_{1\gamma}: \theta \in \Theta_{\gamma}^c ，拒绝域为 \{x: T_r(x) \in W_r\} ，则并-交检验的拒绝区域是 \cup_{\gamma \in \Gamma} \{x: T_r(x) \in W_r\} .
这样做的原理是？要保证 H_0 为真，就需要让每个 H_{0\gamma}: \theta \in \Theta_{\gamma}  都为真；要拒绝 H_0 ，显然只要有一个 H_{0\gamma}: \theta \in \Theta_{\gamma}  被拒绝，则整个 H_0 被拒绝。
\dagger 例：设 X_1, X_2, \cdots, X_n \sim \mathcal{N}(\mu, \sigma^2) 。求下述检验问题 H_0: \mu = \mu_0 \sim H_1: \mu \neq \mu_0  的拒绝域。
解：将这个检验问题的 H_0 写成两个集合的交集： H_0: \{\mu: \mu \le \mu_0\} \cap H_1: \{\mu: \mu \ge \mu_0\}  . 先考虑 H_{0L}: \mu \le \mu_0 \sim H_{1L}: \mu > \mu_0 ，根据似然比检验，拒绝域为 \frac{\overline{X}-\mu_0}{s/\sqrt{n}} \ge t_L ；类似地，对于 H_{0L}: \mu \ge \mu_0 \sim H_{1L}: \mu < \mu_0 ，拒绝域为 \frac{\overline{X}-\mu_0}{s/\sqrt{n}} \le t_U 。因此，整个检验的拒绝域为 \frac{\overline{X}-\mu_0}{s/\sqrt{n}} \ge t_L 或者 \frac{\overline{X}-\mu_0}{s/\sqrt{n}} \le t_U 。当 t_L = -t_U \ge0 时，这个并-交检验的拒绝域可表示为 \frac{|\overline{X}-\mu_0|}{s/\sqrt{n}} \ge t_L 。注意这与似然比检验的结果是一致的。 \dagger
另外一种方法，当原假设可以表示成一个并集时，利用交-并方法 (intersection-union method)。设 H_0: \theta \in \cup_{\gamma \in \Gamma} \Theta_{\gamma}   ，其中 \Gamma 是任意的指标集合，可能有限也可能无限。如果对于每个检验问题 H_{0\gamma}: \theta \in \Theta_{\gamma}  \sim H_{1\gamma}: \theta \in \Theta_{\gamma}^c ，拒绝域为 \{x: T_r(x) \in W_r\} ，则并-交检验的拒绝区域是 \cap_{\gamma \in \Gamma} \{x: T_r(x) \in W_r\} 。原理同样很简单，要拒绝一个并集 H_0 ，需要拒绝并集中的每一个假设，拒绝域是所有拒绝域的交集。
<hr/>参考

• ^Morris H. DeGroot, & Mark J. Schervish. (2010). Probability and statistics: international edition, 4/e.pp454. https://xueshu.baidu.com/usercenter/paper/show?paperid=818c482d9dc8c930bc3cd8a6d2b6ed18&site=xueshu_se
  

原文地址：https://zhuanlan.zhihu.com/p/139386682