金桔
金币
威望
贡献
回帖0
精华
在线时间 小时
|
1 多因子模型简单介绍
预测未来哪支股表现好回报率高,往往需要一个或多个我们可以获得的指标,将它们与未来的股票表现建立联系,进而引导我们的投资。其实质是用变量对股价的波动情况进行拟合,一般而言一个因子是远远不够的。因此今天我们选取多个因子,给它们配以一定的权重合成一个终极因子,用此终极因子来与股票未来收益率建立某种联系,制定出我们的策略,并用历史数据进行检测。
指定多因子策略,我所理解的核心问题就只有两个: <1>哪些因子 <2>因子的权重
2 因子的选取
根据影响市场的情况,我们为了赋予因子可解释的意义,将因子分为以下N类(可能会不全):
<1>估值类因子:PB,PE,PS…代表着市场对于公司价值和表现的预估
<2>盈利类因子:ROA,ROE,Gross Margin…代表着公司的盈利能力
<3>成长类因子:Profit_Growth_Rate,Asset_Growth_Rate…代表着公司的成长能力
<4>波动类因子:股价收益率在一定时间内的标准差…代表着股价的波动情况
<5>情绪类因子:换手率…代表着市场对这支股票的‘情绪’
<6>动量类因子…
<7>分析师类因子…
<8>价值类因子…
在此,我们分别选择EP(市盈率倒数),ROE,TotalProfitGrowRate作为我们的因子(可自行选择),来进行演示。
3 因子的权重
因子的权重有多种分配方式(等权,按照近期IC的平均值,按照线性回归系数,人为分配…)根据你想实现的目的而异。
想追求高收益,低风险,最大回撤小…都有着不同的因子权重分配方式,而且有高人不断探索中…
在此,我们探索目前市场上人们都说的表现极好的一种多因子加权方式:
基于IC的IR最大化(究极因子的IC在过去一段时间的平均值除以IC的方差最大)。
什么意思?假设有n个因子:
在某一时刻

这样得到的多因子权重,可以使得终极因子对于未来收益率的相关性保持比较高而且比较稳的性质。
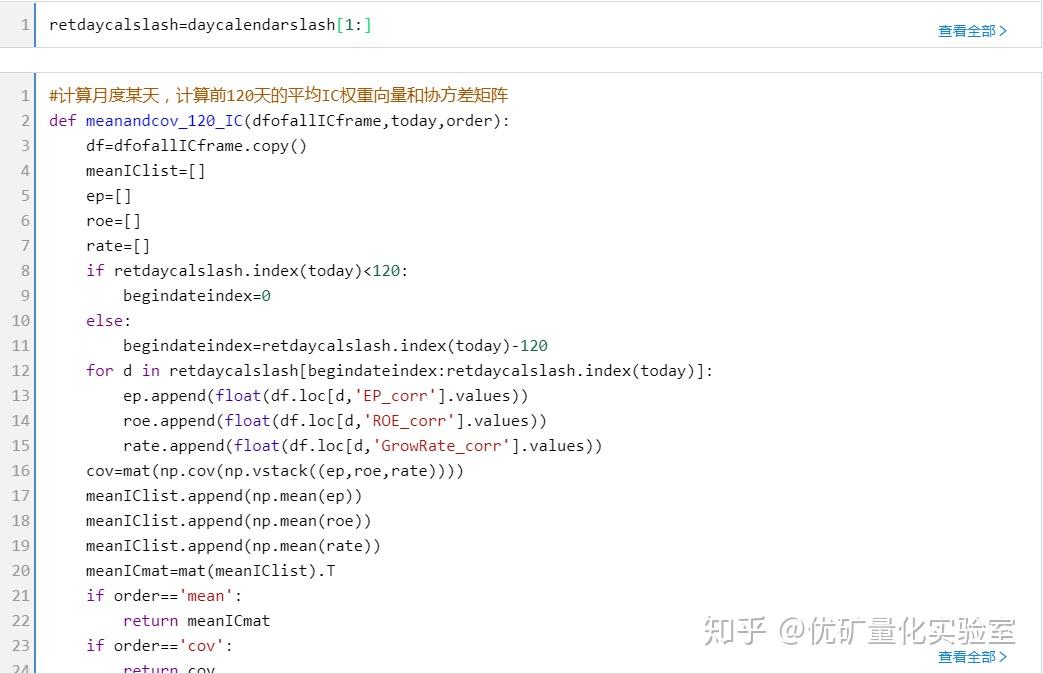
由于我们本次的策略是月度调仓,所以选择过去六个月(120天)来进行某因子IC均值的计算,这样可以保证:
时间不短,协方差矩阵有效反映事实;
时间不长,对于未来不长的时间也有较准确的预测作用。
因此我们来看看代码用这种方法来实现多因子权重的确定以及回测过程。

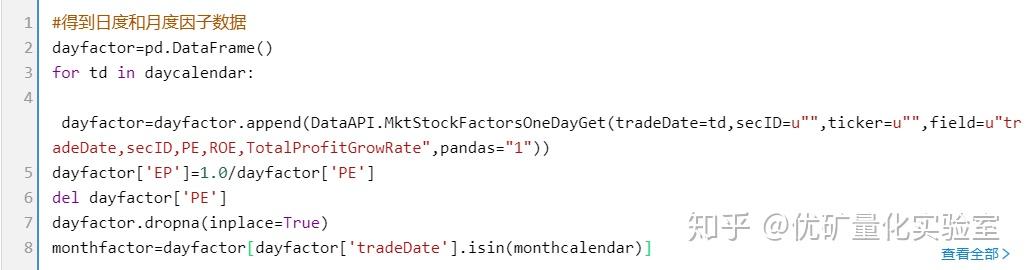
3.1多因子的提取(EP,ROE,TotalProfitGrowRate)
时间时长为2012-06-12到2017-06-12这五年
月度调仓,但是IC按照日度进行计算

查看完整代码请前往优矿量化社区

查看完整代码请前往优矿量化社区

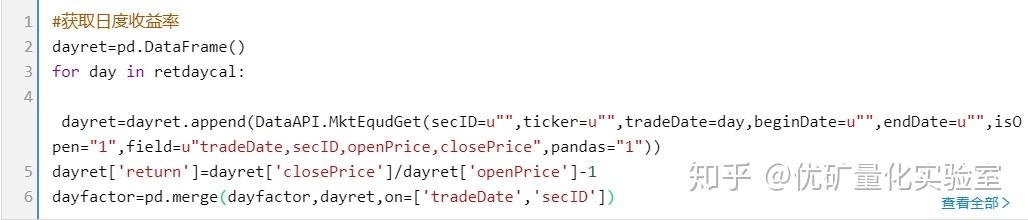
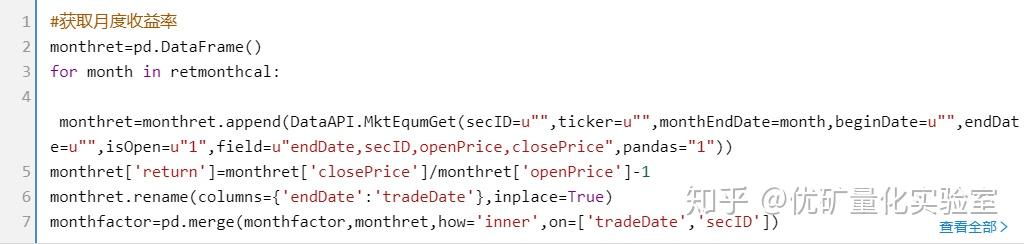
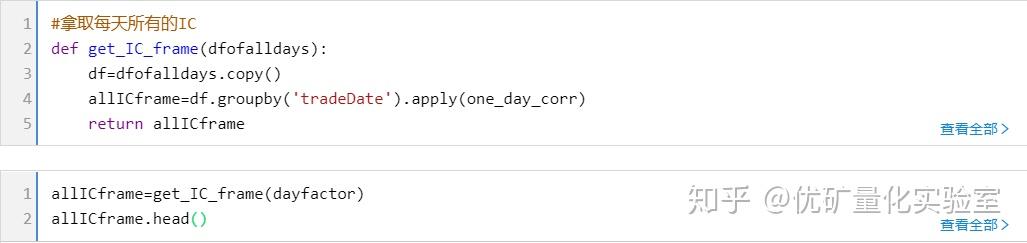
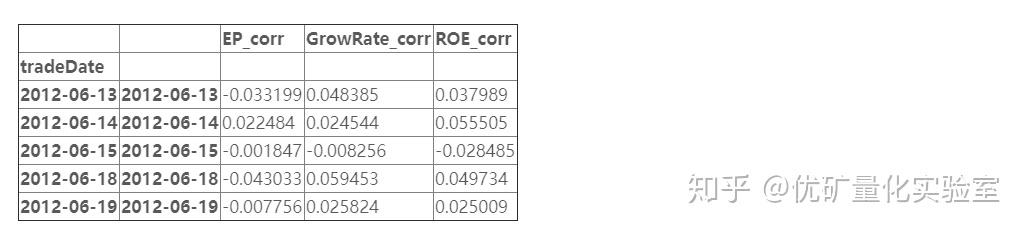
3.2多因子IC(相关系数)的相关计算(pearson系数,按照rank计算)

查看完整代码请前往优矿量化社区
查看完整代码请前往优矿量化社区






查看完整代码请前往优矿量化社区

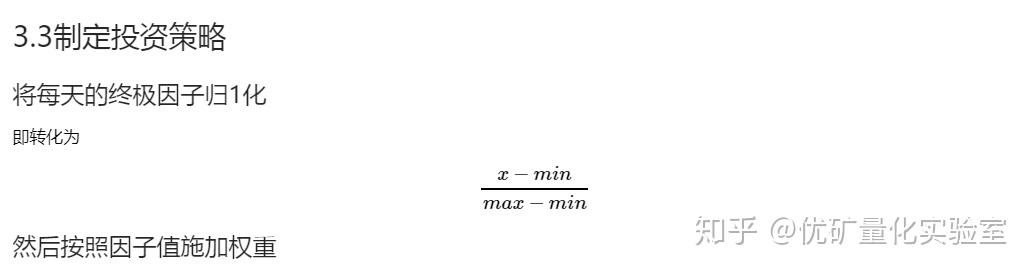


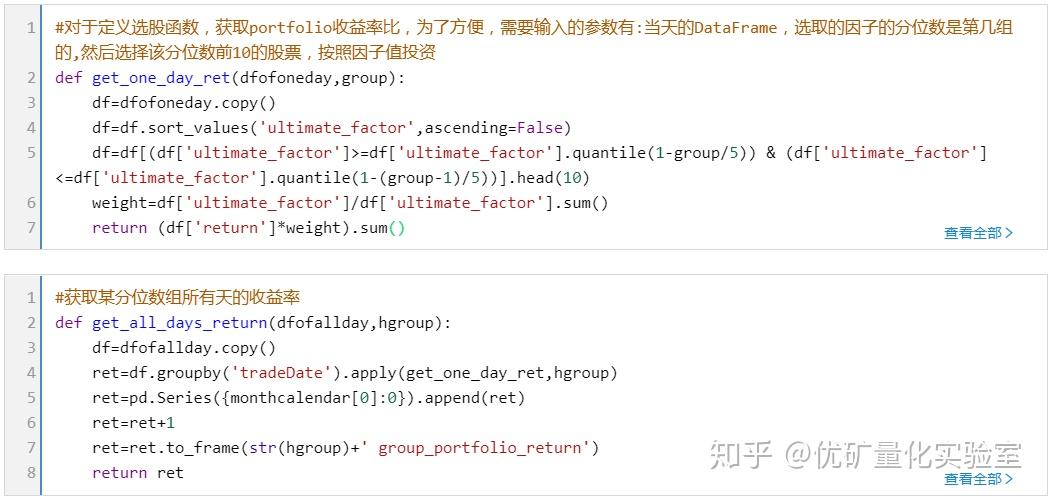
查看完整代码请前往优矿量化社区
3.4计算alpha和beta

查看完整代码请前往优矿量化社区

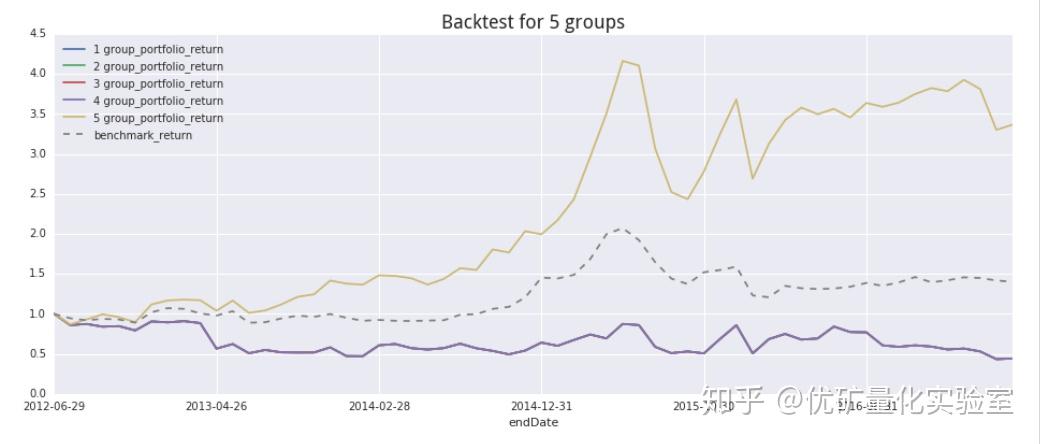
结论:
可以看出,表现最好的是第五组分位数测试,证明这组因子构成的终极因子与未来收益率呈反比关系。
除了第五组和第一组之外,其余组数表现较为接近,还是可以一定程度说明此多因子模型具有比较好的单调性。
对于把因子归1化并按照因子进行投资的方式,只是我为了保证因子在0到1的范围内的一种方法。也可以对因子进行不同角度的处理,从而确定投资权重。
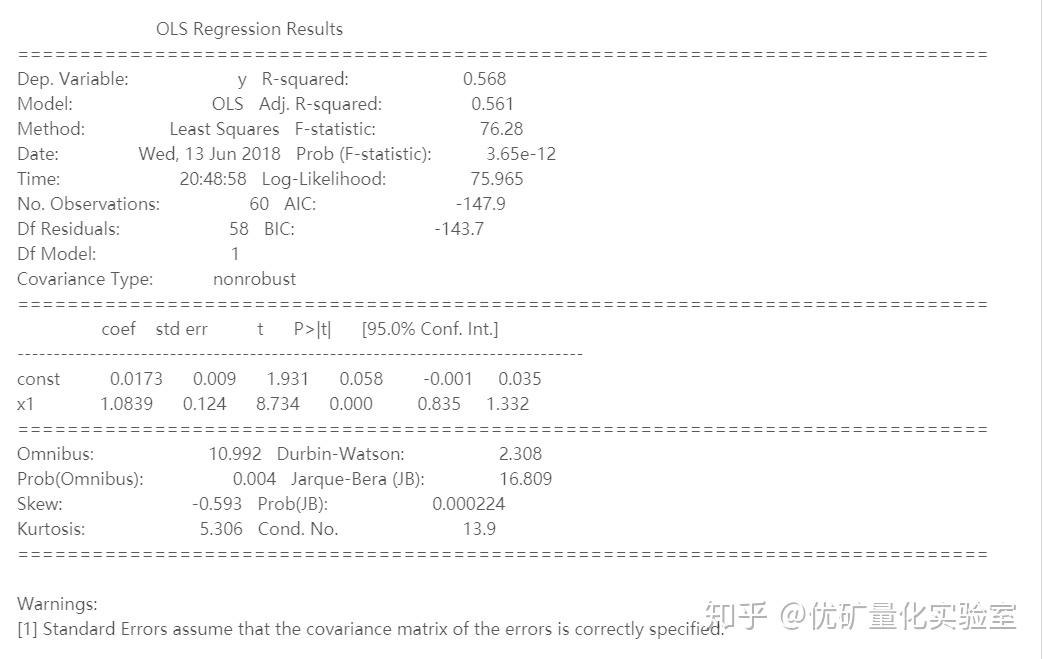
从alpha和beta的计算可以看出,alpha为22%,很大,beta为1.0839,受市场有一定程度的影响。和图像反应给我们的信息是一致的。(alpha很大,而且策略的收益和市场收益很相似。)
总而言之,按照这种加权方式的多因子策略,可能随着因子选择的不同而差异比较大。
但是总得来说,这种加权方式是根据历史最近一段时间内的真实情况给出的权重,对于较短的将来有不小的借鉴意义,表现不会太差。
本文作者:第几个一百天 |
|
 /3
/3 